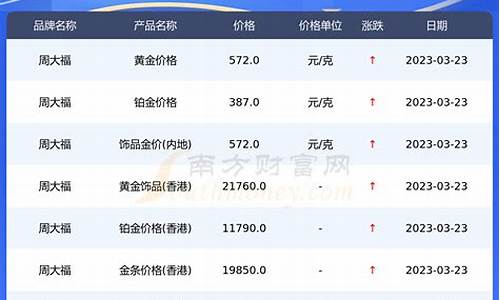
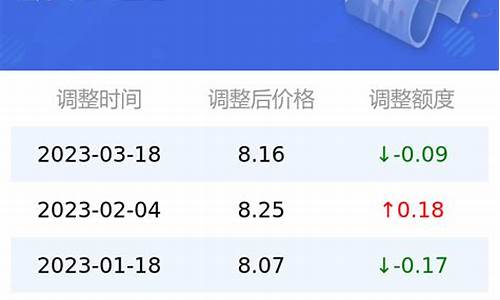
三月油价调整_调整油价3月份的函

1.从蔬菜、肉类、米面油到生活用纸，吃的、用的都涨了！咋回事？

2.预测未来油价改用什么数学建模模型

3.实证研究结果讨论

从蔬菜、肉类、米面油到生活用纸，吃的、用的都涨了！咋回事？

原创出品，禁止抄袭，违者必究。

按照历年的规律来看，3~4月往往是消费的淡季，对应的蔬菜肉类价格走低，但今年是个例外。

一方面是疫情等原因引发的全球通胀开始向下传导到食品端，另一方面俄乌地缘政治冲突加剧了市场看涨的情绪，随着能源、粮食等原料价格上涨，增加了食品成本。

国内不可避免地受到影响，表现为米面油、蔬菜、肉类等价格接连上涨。

1、菜价大涨

当前的菜价确实并不低，有的甚至比肉还贵，就连比较易储存的土豆都涨到了接近3元一斤了，其他不易储存的绿叶菜涨幅就更大了。

比如像黄瓜、蒜苔、菠菜、尖椒等都有比较大的上涨，甚至有的比春节时期还要高。

总体来说，蔬菜的价格上涨主要受3点的影响：

一是一季度以来气温总体偏低，使得蔬菜生长比较缓慢，上市量自然下降；

二是疫情导致的运输受阻，一些蔬菜本身就存在运输不畅的问题，再加上疫情交通受阻，导致产地与市场中断；

三是油价“7连涨”，运输成本无疑也被推高了。

所以最终表现为我们的“菜篮子”越来越“重”了。

2、肉价小涨

相比蔬菜，肉类价格的涨幅并不是太夸张。

比如牛羊肉价格一直坚挺，和春节时期差不多，没怎么降。

而鸡蛋价格也在经历了短暂的回落之后又有了上扬的苗头。

不过，要说便宜的只有猪肉了，受产能高位、消费低迷的影响，猪肉价格确实没怎么涨。

但综合来看，肉价是有小幅上涨的。

而肉价上涨的主要原因还是受疫情影响运输不畅，使得产销不均，产地往往价格便宜，而销区却较贵。

3、米面油涨了

在米面油中，涨幅最大的就要数食用油了。

随着俄乌冲突的持续，乌克兰暂停了葵花籽油的出口。

而乌克兰的葵花籽油出口量占全球的80%，因此一旦暂停影响较大，全球多国出现了“油荒”。

比如西班牙已经开始对食用油进行了限购，每人只能购买5升，而印尼也开始排队抢购食用油。

而国内方面，无论是大豆油还是葵花籽油，与去年同期相比涨幅也都超过了50%。

米面的价格也有小幅上涨。

尤其是今年小麦价格可谓是频频上涨，最高时突破了1.7元/斤，这在历史上还是首次，因此带动面粉价格也有一定涨幅，一袋面粉涨了约20-30元。

不过鉴于米面是绝对的口粮，而这种涨幅主要是成本增加导致的，并不是供求关系的波动，因此后续上涨的空间基本很小了。

4、生活用纸也涨了

随着吃喝上涨，一些生活用品也出现了上涨，例如生活用纸。

3月底时，各大纸业纷纷发布了调价函，文化纸和生活用纸都出现了上涨。

例如，晨鸣纸业在3月底时宣布将其系列产品价格上调300元/吨，而太阳纸业也将生活用纸原纸的出货价格上调了300元/吨，累计近一个月内涨幅达到了500元/吨。

纸张上涨的原因主要是上游木浆价格上涨引起的。

中国对进口纸浆依赖度较高，木浆进口的依存度就在60%以上。

而受全球市场波动以及能源价格走高的影响，根据国家统计局监测，3月上旬时，全国流通领域纸浆价格为7009.8元，相比1月份上旬时为6111.6元，2月内涨幅就达到了14.7%。

不过，生活用纸经常会搞促销活动，所以对大众来说，对于价格上涨并不敏感，而肉类也因为消费低迷所以也感觉不明显。

但是人们普遍对于菜价的上涨有比较明显的感觉，不过蔬菜的上涨往往很难持续，后续随着天气的回暖，上市量的增加，这种局面会得到一定的缓解。

欢迎收藏“新农观”，一起了解新时代下三农的新发展。

预测未来油价改用什么数学建模模型

建议用BP神经网络，并且结合主成分分析法。

一些常用的方法，比如多元回归和时间序列方法构建价格预测模型，是一种典型的线性预测模型，能够预测价格变化的线性关系，对中长期预测具有一定的局限性。

神经网络是一种智能预测方法，需要对对象建立准确的数学模型，能够准确描述对象的特征，具有学习能力强、并行处理等特点，在复杂系统等领域的建模中得到了广泛的应用，也为石油价格预测提供了思路。但是由于影响石油价格的因子比较多，且数据中含有噪声，直接采用神经网络学习收敛速度慢，且预测精度低，因此需要对石油价格影响因子预处理。针对石油价格变化的特点，提出一种基于主成分分析和BP神经网络的石油价格预测模型。该模型采用定性分析选择出影响因子，再利用主成分分析方法对石油价格影响因子进行筛选，选取最主要的几个影响因素，最后通过神经网络能够逼近非线性连续函数的能力对石油价格进行预测，从而实现了石油价格的准确预测。

价格的预测过程

BP神经网络的预测过程如下：

1、收集石油价格以及影响因子，并获取相关数据。

2、对石油价格影响因子进行主成分分析，并筛选出贡献率大的主成分。

3、将石油价格数据分为训练样本和预测样本。

4、采用BP神经网络对训练样本进行训练，并找出模型的最优参数。

5、利用最有参数建立BP神经网络预测模型，对预测样本进行预测。

实证研究结果讨论

4.5.3.1 基本统计分析

令POt,PEt分别表示第t日WTI国际原油价格和欧元对美元汇率价格，其统计特征如表4.23所示。不难发现，首先，两个价格（汇率也可以看做一种相对价格）序列都是非正态分布的；其次，两个价格序列都存在显著的自相关性和异方差性，因此存在显著的波动集聚性。还有，ADF检验结果表明，在5%的显著性水平下，两个价格序列都是非平稳序列，但都是一阶单整序列。从两者的标准差也可以发现，总体而言油价波动的风险比汇率波动风险要大。

表4.23 国际油价和美元汇率序列的基本统计特征

4.5.3.2 均值溢出效应检验

（1）协整性分析

为了利用长期弹性的概念，我们先对两个价格序列取自然对数，得到两个新的变量1n_PO和1n_PE。由于国际油价和美元汇率序列取自然对数后仍然均是一阶单整序列

检验结果表明，取自然对数以后，两个价格序列仍然是一阶单整的，符合应用协整理论的基本要求。具体统计检验结果可向作者索要。

国外油气与矿产资源利用风险评价与决策支持技术

式中：括号内为相应变量的t统计量值；**表示在1%的显著性水平下显著。采用ADF方法检验回归方程残差项εt的平稳性，结果发现，残差序列在1%的显著性水平下是显著平稳的。因此，我们认为国际油价和美元汇率之间存在长期均衡的协整关系。而从协整回归系数看到，两者之间存在的均衡关系是正向的。并且，国际油价关于欧元对美元汇率的长期弹性系数为1.26，即美元汇率变动1%，国际油价长期来看平均变动1.2607%。可见，两个市场之间的长期互动关系非常显著，因此在分析和预测国际油价长期走势时，美元汇率的变化必须考虑。

（2）跨期互相关检验

尽管国际油价和美元汇率都不是平稳序列，但它们之间存在协整关系，因此符合建立VaR模型的先决条件。而为了确认是否需要采用VaR模型建模，我们先检验国际油价序列和美元汇率序列的跨期互相关性，滞后2阶时，得到跨期互相关系数如表4.24所示。可见，油价和汇率序列之间滞后2期的互相关系数都较大，这说明两个市场的条件均值之间存在显著的引导和滞后关系。因此，建立VaR模型很有必要。

表4.24 国际油价和美元汇率之间的跨期互相关系数

（3）均值溢出效应检验

通过对油价和汇率两个序列建立VaR模型，根据模型的整体AIC值最小准则，求得Granger因果检验的最佳滞后阶数为1，从而得到Granger因果检验结果如表4.25所示。从显著性概率发现，欧元对美元汇率是国际油价波动的Granger原因。而国际油价变化并不是显著引起美元汇率起伏的Granger原因。因此可以认为，存在从美元汇率到国际油价的单向均值溢出效应，即国际油价的变化受前期美元汇率变化的显著影响。

表4.25 油价和汇率的Granger因果检验结果

自2002年起，美元持续贬值，原因非常复杂，其中最根本的原因在于美国政府试图有效拉动出口，缩减贸易赤字。另一方面，受到市场供需、地缘政治和金融市场等因素的综合影响，国际油价自2002年起也连创新高。通过上述均值溢出效应检验，我们可以认为，美元的贬值对国际油价上涨存在显著的推动作用。这是由于原油期货交易主要以美元计价，而美元贬值导致部分外国投资者大量买进原油期货交易合约以获取更高利润，而原油期货价格的走高势必导致现货价格的上扬。当然，这里面也暗含一种长期影响的意义。

与前人采用实际油价和实际汇率计算得到的结果相比，采用名义价格得到的结果表明，尽管从长期而言油价和美元汇率之间仍然存在一种均衡的互动关系，但是相互影响的方向发生了变化。因此可以认为，物价水平一定程度上改变了两个市场之间的长期互动关系。

（4）脉冲响应函数结果分析

在VaR 模型中，脉冲响应函数可用于衡量来自随机扰动项的一个标准差冲击对变量当期和未来取值的影响。基于国际油价与美元汇率建立的脉冲响应函数如图4.27所示。可见，美元汇率一个标准差（对数值为0.1463，对应原始汇率的0.1557）对国际油价的影响是缓慢增加的，在大约1年以后（具体结果为234天）达到最大程度0.00879美元/桶（此为对数值，转换成国际油价为1.0088美元/桶），并趋于平稳减缓；而国际油价的一个标准差（对数值为0.2422美元/桶，对应原始油价为8.3743美元/桶）对美元汇率的影响较为微弱，接近于0。这种结果进一步验证了国际油价和美元汇率之间的单向均值溢出效应。

图4.27 国际油价与美元汇率的脉冲响应函数

a—油价受到冲击后的反应；b—美元汇率受到冲击后的反应

4.5.3.3 波动溢出效应检验

（1）价格序列的GARCH效应分析

从表4.23中看到，两个价格的平方序列均存在显著的序列相关性，即原序列具有显著的波动集聚性，因此我们引入ARCH 类模型刻画这种性质。考虑到序列的自相关性，因此主体模型采用随机游走模型。通过检验残差的ARCH 效应，我们发现，国际油价序列存在显著的高阶ARCH 效应，因此考虑采用GARCH 模型，然后按照AIC值最小的准则，多次尝试，决定采用GARCH（1,1）模型来描述国际油价序列的波动集聚性。另外，考虑到实证研究结果表明油价上涨和下跌带来的价格波动并不对称，因此考虑采用TGARCH 模型，通过模型的AIC 值发现，这样的做法也是合理的。检验TGARCH模型残差的ARCH 效应，发现ARCH 效应已经滤掉，而且，Q（10）和Q2（10）统计量的检验结果也表明模型残差不再存在额外的序列相关性和波动集聚性，这说明TGARCH（1,1）模型对国际原油价格波动特征的拟合效果较好。同理，我们发现GARCH（1,1）模型能较好地刻画欧元对美元汇率的波动集聚性。模型参数估计结果如表4.26所示。

表4.26 国际油价和美元汇率的（T）GARCH模型参数估计结果

需要说明的是，考虑到模型的残差都不服从正态分布，因此我们采用基于GED分布的（T）GARCH模型描述模型残差的尖峰厚尾特征。表4.23结果显示，GED分布的参数均小于2，从而验证了使用（T）GARCH模型对油价和美元汇率序列建模时所得残差项的厚尾特征。

波动模型的参数估计结果表明，国际油价的波动具有显著的不对称性，即杠杆效应。杠杆系数为负，表示相同幅度的油价上涨比油价下跌对以后油价的波动具有更大的影响。具体而言，油价下跌时， 对ht的影响程度α1＋Ψ为0.0219；而油价上涨时，该影响程度α1为0.0688，是油价下跌时的3.1倍左右。产生这种杠杆效应的原因是多方面的，石油的不可再生性是其中最根本的原因，它决定了石油供给者的市场地位明显高于石油需求者。因此，油价上涨会加剧石油短缺的预期，使市场交易者倾向于在当期购买。这种争夺加剧了油价的进一步上扬，加上市场投机因素的推波助澜，促使油价上涨时波动程度格外突出。而油价下跌时，石油生产商减少开采量，石油经销商囤货待售，导致市场供给量降低，油价出现回升，阻碍了其进一步下挫。可见，石油市场多空双方的不对称地位决定了供给不足时油价的上涨幅度要大于供给过剩时油价的下跌幅度，从而造成了石油市场的上述杠杆效应。

从波动模型也可以发现，美元汇率的波动存在显著的GARCH 效应。方差方程中 与h t-1前的系数之和α1＋β1刻画了波动冲击的衰减速度；其值越靠近1，则衰减速度越慢。在本节的GARCH（1,1）模型中，该系数之和为0.9872，说明美元汇率具有有限方差，即属于弱平稳过程。美元汇率的波动最终会衰减，但可能会持续较长时间。其中ht-1前的系数为0.9533，表示当期方差冲击的95.33%在下一期仍然存在，因此半衰期为14天。

（2）波动溢出效应检验

按照前文的波动溢出效应检验模型，得到国际油价与美元汇率之间波动溢出效应估计结果，如表4.27所示。我们发现，从统计上讲，国际油价和美元汇率的y系数都不显著。可见，尽管国际油价和美元汇率之间存在长期均衡的协整关系，也有显著的单向均值溢出效应；但是它们之间的波动溢出效应并不显著，即双方的价格波动信息具有一定的独立性，价格波动程度的大小不会显著互相传递。这也表明，从价格波动态势的角度讲，美元汇率对国际油价的影响相当薄弱。

表4.27 国际油价与美元汇率的波动溢出效应检验结果

4.5.3.4 风险溢出效应检验

市场有波动不代表一定有风险，因此风险溢出效应是波动溢出效应的一种拓展。按照VaR的计算思路，本节采用国际油价分布函数的左分位数来度量油价下跌的风险，表示由于油价大幅度下跌而导致的原油生产者销售收入的减少；而采用分布函数的右分位数来度量油价上涨的风险，表示油价大幅度上涨而导致的原油采购者的额外支出。这种全面考虑市场风险的思路同样适用于美元汇率市场。就本节采用的欧元对美元汇率而言，汇率的涨跌将在多个方面给国际汇率市场的不同主体产生不同的风险。比如就发生在美国本土的国际进出口贸易而言，汇率下降表示美元升值，美国出口商和欧元区的进口商将面临较大风险；汇率上升表示美元贬值，则美国进口商和欧元区的出口商就可能面临明显的市场风险；而就石油美元而言，美元升值，将额外增加石油进口国（如欧元区）的开销；美元贬值，又会给主要石油出口国（如OPEC）的石油销售收入形成阻碍。

综上所述，石油市场和美元汇率市场都需要同时度量价格下跌和上涨的风险，从而为市场不同参与主体提供决策支持。本节将采用上述基于GED分布的TGARCH（1,1）模型和GARCH（1,1）模型，按照方差－协方差方法来分别度量国际油价和美元汇率在价格上涨和下跌时的VaR 风险值，并检验两个市场之间的风险溢出效应。

（1）GED分布的分位数确定

根据GED分布的概率密度函数，使用MATLAB编程，经过多次数值测算，求出GED分布在本节所得自由度下的分位数（表4.28）。表中结果显示，95%的分位数与正态分布的1.645基本相同，但99%的分位数却明显大于正态分布的2.326，这也表明国际油价和美元汇率价格都具有严重的厚尾特征。

表4.28 国际油价和美元汇率价格的GED分布参数及分位数

（2）基于GED－（T）GARCH模型的VaR风险值计算

根据上述VaR 风险的含义，按照方差－协方差方法，我们得到以下两个计算VaR风险的公式。价格上涨风险的VaR值计算公式为：

国外油气与矿产资源利用风险评价与决策支持技术

式中：μm,t为第m个市场第t日价格的条件均值（即实际值与残差的差），zm,a为第m个市场中（T）GARCH（1,1）模型的残差所服从的GED分布的右分位数；hm,t为第m个市场价格的异方差。

同理，得到价格下跌风险的VaR值计算公式为

国外油气与矿产资源利用风险评价与决策支持技术

基于上述计算公式，本节计算了在95%和99%的置信度下，国际油价和美元汇率的上涨风险和下跌风险。经过LR检验（Kupiec,1995），我们发现VaR 风险的结果是可靠和可行的。

（3）风险溢出效应检验

得到国际油价和美元汇率价格上涨和下跌时的VaR风险值之后，我们根据Hong（2003）提出的风险－Granger因果检验方法，构造相应的统计量Q1（M）和Q2（M），并通过M ATLA B编程求出统计量的值及其显著性概率，从而检验石油市场和美元汇率市场之间的双向和单向风险溢出效应。计算结果如表4.29所示，其中M分别取10,20和30。

从风险检验结果看到，从下跌风险角度（即油价下跌，美元升值）看，国际石油价格与美元汇率之间存在双向风险溢出效应，进一步检验单向风险溢出效应，发现在95%的置信度下，存在从美元汇率市场到国际石油市场的风险溢出，而并不存在从国际石油市场到美元汇率市场的风险溢出效应。可见，美元汇率升值的风险对国际油价下跌的风险影响显著。而在99%的置信度下，国际油价和美元汇率之间并不存在任何方向的风险溢出效应。因此可以认为，就下跌风险而言，两个市场之间的风险溢出效应比较有限，当准确性要求提高到一定程度时，美元汇率升值对油价下跌的风险影响可以忽略。

表4.29 国际油价与美元汇率价格风险溢出效应检验结果

另一方面，从上涨风险角度（即油价上涨，美元贬值）看，不管是在95%还是99%的置信度下，两个市场之间都不存在任何方向的风险溢出效应。可见，近些年来，虽然美元总体上持续贬值，但就市场风险而言，这种贬值并未给国际原油价格的上涨风险带来显著的推动作用。换言之，尽管国际油价高企导致国际石油市场的主要采购者（如中国和印度）的购油额外支出明显增加，但美元持续贬值并不是这些国家支出增加的显著原因。

总体而言，我们需要特别关注美元升值对国际油价走低的风险作用，采取积极手段，有效规避市场风险。近些年来，尽管从每日交易的角度而言，美元汇率时有涨落。但总体而言，美元贬值是大趋势，欧元对美元汇率连创历史新高，这种趋势并没有给油价上涨风险产生显著的影响。因此，在这种大环境下，对市场交易者而言，风险溢出效应的实证结果是一个满意的信号。